Dynamic Memory Allocation Part2

In the previous post I covered a generic, but rather simplistic approach to dynamic memory allocation. The approach covered there is legitimate, but isn’t particularly fast and I don’t think it gets a lot of practical use.

In this post I’d like to cover a rather interesting algorithm, that on the one hand is not as generic as the one I covered in the previous post, but on the other hand it’s quite often used in practice.

As always the code is available on GitHub.

Introduction

The algorithm I will cover is refered to as Buddy Allocator or Buddy System. As I mentioned the algorithm I’ll cover here is not generic, so what does it mean?

This algorithm will allocate memory only by powers of two. So if you want to allocate a memory range you’d have to round the size up to the closest power of two that is large enough.

Additionally, even though it’s not strictly a limitation of the algorithm, due to the amount of metadata we will maintain this algorithm is somewhat wasteful for allocation of small memory blocks. As a result, we will not be working with individual bytes and sizes in bytes, instead we will be working with pages and sizes in pages.

The page size can be anything, but, to give you an example, a potential page size might be 4096 bytes. So algorithm can allocate 1 page, 2 pages, 4 pages and so on.

Moreover, instead of working with the allocated memory directly, I will create a representative (handle, descriptor, etc) for each page. Each representative will contain some amount of metadata that the algorithm will use to maintain its state.

As a result, the interface of the algorithm will look something like this:

struct BuddySystem {
    /* fields */
}

impl BuddySystem {
    pub fn allocate_pages(&mut self, order: u64) -> Option<u64> {
        /* implementation */
    }

    pub fn free_pages(&mut self, index: u64) {
        /* implementation */
    }
}

In this interface index is the number of the page, so you can convert from the index to the address easily by multipling by the page size and vice versa. The order is the power of two. So, for example, allocate_pages(2) will try to allocate a contigous block of four pages. If the allocation is successful it will return the index of the first page in the block.

Hopefully that high level introduction will give you a general idea of what kind of beast we are going to release, so let’s get down to it.

Page

I’ll start with introducing a page representative. There are few pieces of information that we will have to keep per page. One obvious piece is whether the page is free or busy.

In addition to that we will have to store order or level of the page. It’s a little bit hard to explain what this field will actually mean at the moment, but I’ll cover it in details later. For now, all you need to know that level of the page is a small number. When it comes to memory allocation, it doesn’t make sense for this number to be more than 64, so it can easily fit in one byte.

Finally, we will be linking page representatives in lists. In order to do that we need to have fields for the next and previous elements of the list.

All in all we are getting something like this:

use core::cell::Cell;

pub struct Page {
    pub next: Cell<*const Page>,
    pub prev: Cell<*const Page>,
    level: Cell<u8>,
    free: Cell<bool>,
}

I use *const Page instead of something like Option<&Page> here because being able to initialize the structure with zeros is quite a convenient property to have, but in Rust references can never be null. I suspect that Option<&Page> can be zero-initialized, but I could not find any kind of guarantees about that, thus I do not depend on that.

I wrapped all the fields into core::cell::Cell. Cell essentially allows to modify data via immutable reference. And yes, it’s safe as far as Rust type system is concerned.

The reason to do it this way, is because without that the only way to modify the fields would be to either drop to unsafe code or via mutable references.

The problem with mutable references is that you’re only allowed to have one of those at a time. That’s problematic if you have to maintain more than one reference to an object (like for example, in doubly linked lists, or in general when you want to have multiple different indexes refereing to the same objects).

We are not done with the Page structure just yet. You see, we will create a separate Page structure for each page of the memory we will be working with. So naturally, the bigger the structure size, the more overhead we will have. So it might make sense to compress it a little bit. After all free and level can easily fit in one byte - there is no reason to create multiple fields for them and pay for field alignment overhead.

Here is what I ended up having in the end:

use core::cell::Cell;
use core::ptr;

pub struct Page {
    pub next: Cell<*const Page>,
    pub prev: Cell<*const Page>,
    state: Cell<u64>,
}

const LEVEL_MASK: u64 = 0x7f;
const FREE_MASK: u64 = 0x80;

impl Page {
    // This function is only useful for tests, as Page structure will normally
    // be initialized with zeros without calling Page::new().
    pub const fn new() -> Page {
        Page {
            next: Cell::new(ptr::null()),
            prev: Cell::new(ptr::null()),
            state: Cell::new(0),
        }
    }

    pub fn level(&self) -> u64 {
        self.state.get() & LEVEL_MASK
    }

    pub fn set_level(&self, level: u64) {
        assert_eq!(level & ~LEVEL_MASK, 0);
        self.state.set(level | (self.state.get() & !LEVEL_MASK));
    }

    pub fn is_free(&self) -> bool {
        (self.state.get() & FREE_MASK) != 0
    }

    pub fn set_free(&self) {
        self.state.set(self.state.get() | FREE_MASK);
    }

    pub fn set_busy(&self) {
        self.state.set(self.state.get() & !FREE_MASK);
    }
}

Rust doesn’t really provide much guarantees about the internal layout of structures. but if it’s any kind of sensible, then I’d expect that Page structure to be 24 bytes long. With the 4096 byte pages it gives us 0.6% overhead.

To compare, the algorithm from the previous post had about 32 bytes overhead per allocated memory block after applying similar compaction. Though keep in mind that algorithm only incures overhead for blocks of memory we actually allocated, which is not the case for the Buddy System. For the Buddy System we will have to reserve all the memory we need for the metadata upfront, so we always paying this overhead.

List

We need to be able to link Page structures in lists. I will not cover the list implementation, as it’s hardly interesting and nobody would benefit from another bespoke linked list implementation.

Instead I just cover what operations we need and some important properties of the implementation.

Basically, we need just three operations: push, pop and remove. Push and pop are more or less self explanatory: push adds element to the list and pop returns an element from the list. From the algorithm point of view the order of the elements in the list doesn’t matter.

Remove operation given an element of the list and the list itself unlinks the element from the list. The linked list in this case doesn’t own any of the elements it stores, so it cannot delete, copy or move the elements around and restricted to only work with the prev and next fields of the Page structure.

Without covering the implementation here is the interface I ended up with:

use core::option::Option;

pub struct List<'a> {
    head: Option<&'a Page>,
}

impl<'a> List <'a> {
    pub const fn new() -> List<'a> { /* implementation */ }

    pub fn is_empty(&self) -> bool { /* implementation */ }

    pub unsafe fn push(&mut self, page: &'a Page) { /* implementation */ }

    pub unsafe fn pop(&mut self) -> Option<&'a Page> { /* implementation */ }

    pub unsafe fn remove(&mut self, page: &'a Page) { /* implementation */ }
}

Since we use pointers for the linked list links and to implement the operations we need we have to dereference them, the implementation will necessarily use unsafe Rust. I did keep the unsafe in the interface and didn’t try to hide it because with the way the Page structure is defined and how List links Page structures together all the safety guarantees Rust provides are out of the window anyways. Trying to hide it would be rather misleading.

Buddies

We are done with preparations, it’s now time to get to the meat of the algorithm itself. The main idea of the algorithm and the origin of the name is that we will statically pair pages together. To put it another way, we will be creating buddies.

For example, pages with index 0 and 1 are going to be buddies, pages 2 and 3 will be buddies, pages 4 and 5 will be buddies as well and so on - you probably can see the pattern.

More formally, though for the page with index \(x\) the index of its buddy will defined the following way:

\[buddy = x \oplus 1\]

where \(\oplus\) is bitwise exclusive or operation. In other words, to find the index of the buddy we need to flip the least significant bit of the index.

You can easily check that it works for the examples given above. Note however, that according to this formula pages with index 1 and 2 are not buddies even though they are neighbours.

NOTE: keep in mind that not all pages may have buddies, for example, if you have only 7 pages, due to the odd number of pages, at least one page will not have a buddy.

Now I’m going to take this idea of buddies and generalize it a little bit. We know that two buddy pages must be neighbours - that’s just how the formula above works.

We can combine two buddy pages in a bigger page. For example, pages with index 0 and 1 are buddies and together they can form a contigous block of a higher order or level. You might catch a drift at this point of what the level in the Page structure is for.

We will call individual pages blocks of order or level 0, as if they are \(2^0 = 1\) pages long. Two buddy pages combined form a block of level 1, as if it’s \(2^1 = 2\) pages long. Similarly we can combine two buddy blocks of level 1 into one block of level 2, and so on and so forth.

For each block, we will use the page with the smallest index as a representative. For example, when we combines pages 0 and 1 we will get a block of level 1. In that block the page with the smallest index is 0 and this page will be representative of the block.

It’s not hard to generalize the formula above to the blocks of arbitrary levels. Let’s say we have a block of level \(level\) that is represented by page \(x\), to find the buddy of that block we can use the following formula:

\[buddy = x \oplus 2^{level}\]

For example, for the block 0 of order 1 (meaning 2 pages long block) the buddy index will be 2. For the block 4 of order 1 the buddy index will be 6 and so on.

If you draw a picture you may see that buddies form some kind of a tree structure:

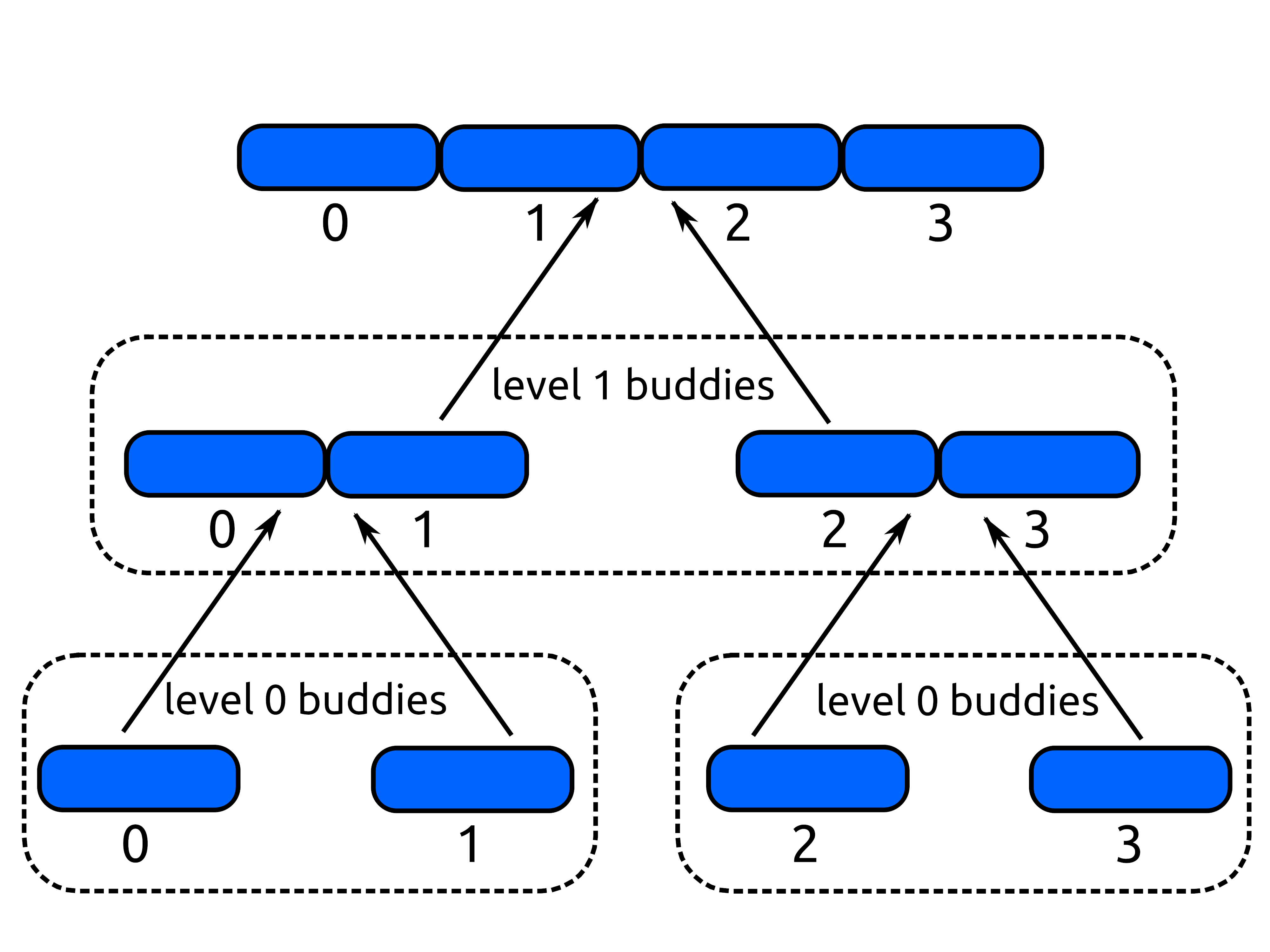
So why do we need to pair memory blocks this way?

In the previous post we spent a great deal of time figuring out how can we combine adjusent free memory ranges effectively in bigger memory ranges to avoid fragmentation.

In the Buddy System we will do the same, but we will not combine arbitrary adjusent blocks together. Instead we will only combine buddies together.

Combining two free buddies together gives us a bigger memory block. Buddy of that bigger memory block might also be free. If so we combine them into even bigger memory block and so on.

Similarly when we are allocating memory, we have to find a large enough memory block and split it until we are left with the block of just the right size. When we split one big block in two and we endup with two buddies. One of the buddies is returned to the allocator and stays free, while we continue to work with the other buddy.

Allocating pages

Now when we have an idea of what buddies are we can get to the allocation algorithm using the Buddy System. First let me start with introducing the structure:

pub const LEVELS: usize = 20;

pub struct BuddySystem<'a> {
    free: [List<'a>; LEVELS],
    pages: &'a [Page],
}

NOTE: Here I assume that the memory for the Page structure was allocated somehow and here we just have a reference to the slice containing the Page structures - that simplifies the description of the algorithm. You can reserve memory for the pages from the memory that the Buddy System manages, just don’t forget to make sure that this memory is marked as busy, so that you will not allocate it to somebody.

For each possible level we have a separate list. As the name of the field suggests we will be keeping free blocks in those lists.

I limit the number of levels to 20 here. It means that the largest block that my implementation will consider will have level 19, or, in other words, it will be \(2^{19}\) pages in size.

It’s an arbitrary restriction that I’ve put in place. You can increase the limit higher than that - there is no problem with that. When it comes to the memory allocation, it hardly makes sense to work with blocks larger than \(2^{64}\), so this number cannot be too big anyways.

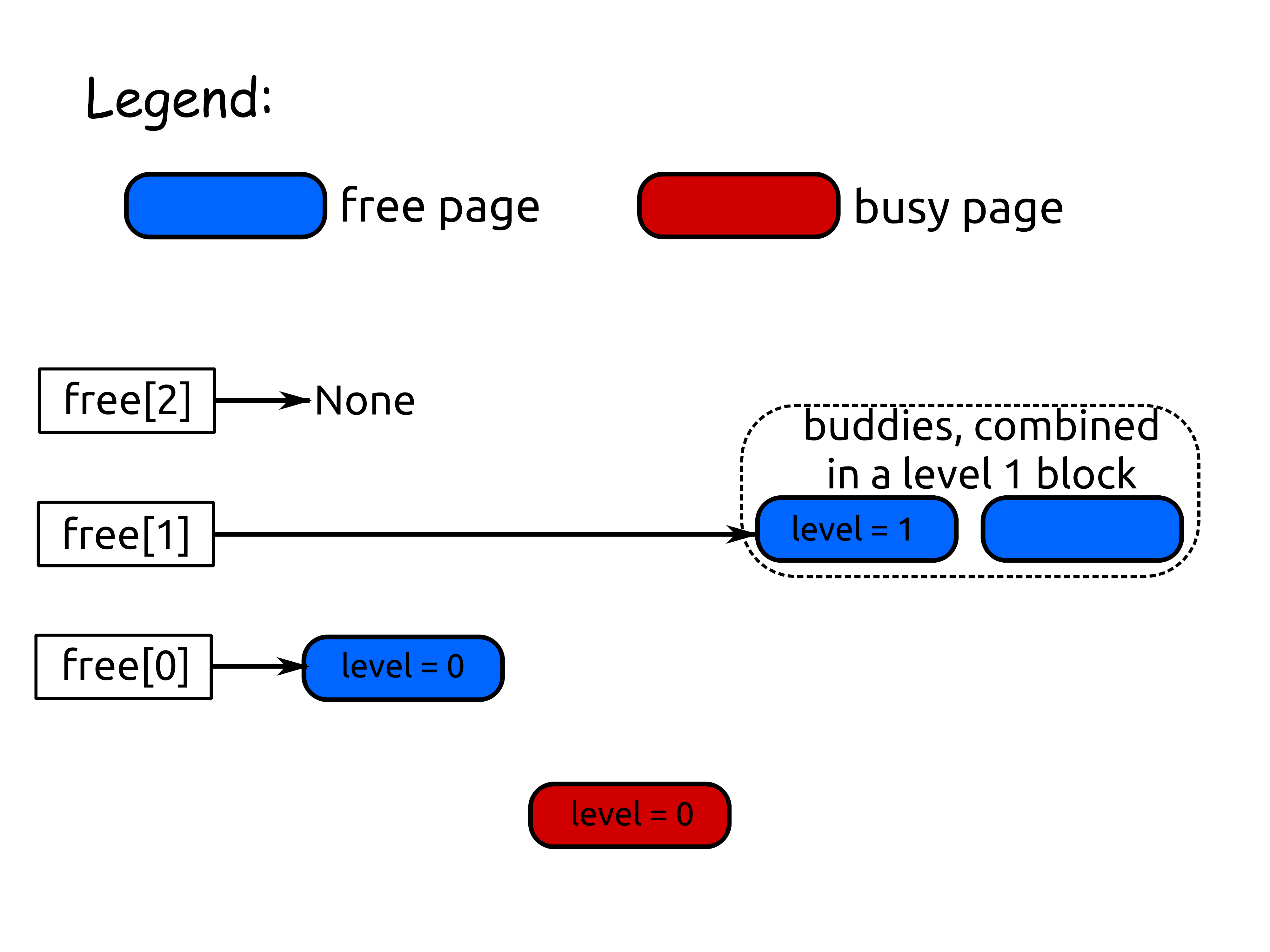
Initial State

I’ll start explanation of the allocation alogrithm from giving you some intuation of how the state is tracked in the Buddy System.

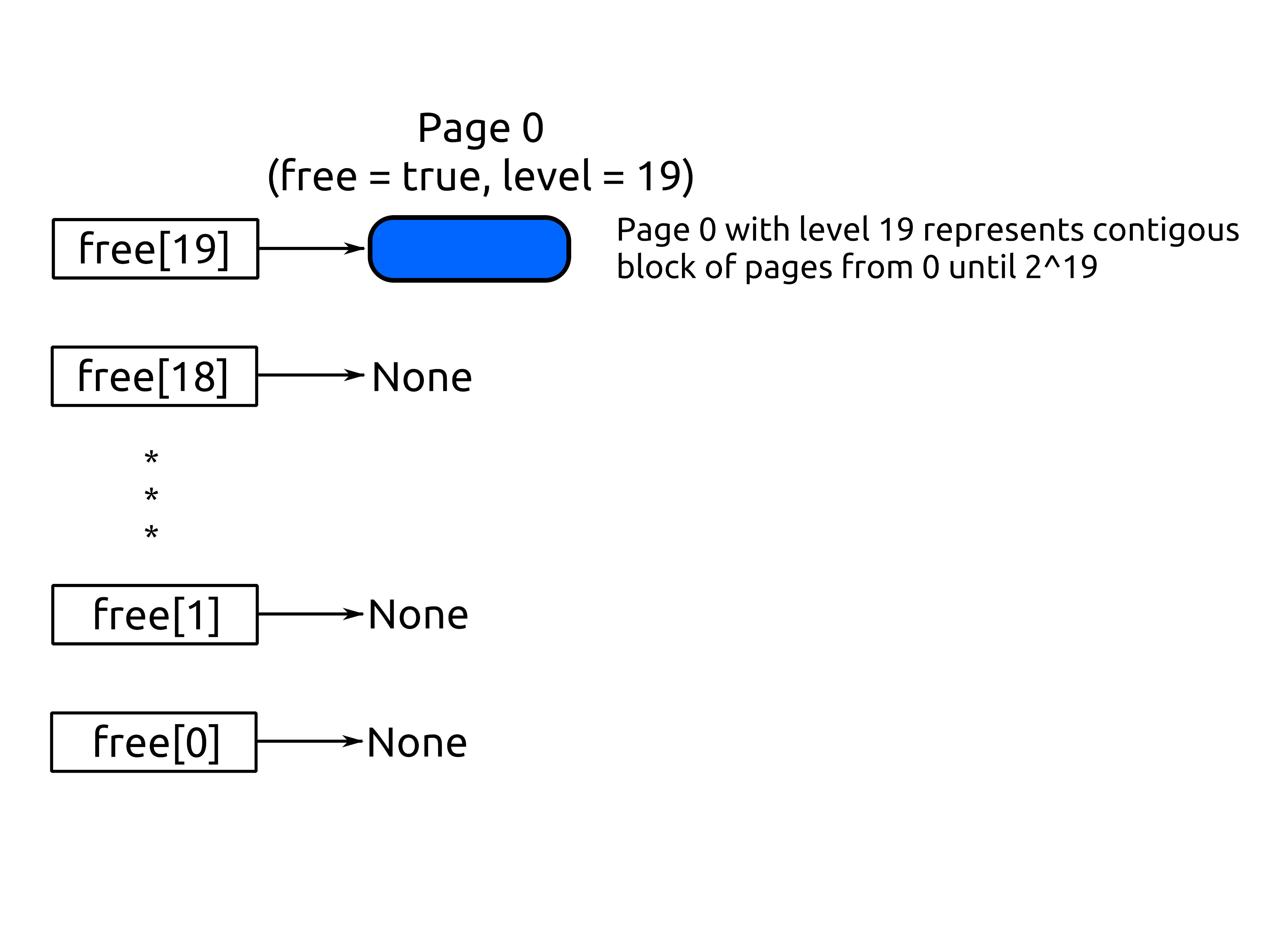
To be specific and without loss of generality, let’s assume that we have exactly \(2^{19}\) pages of memory and all of those pages are free. How the Buddy System state would look in this case?

In this state all lists in the free array except the last one will be empty, but the last one will contain just one entry - page 0.

That means that all memory we have combined in one big block of level 19 and page 0 is the representative of this big block. The Page structure of the page 0 in this state should be marked as free and have level set to 19.

In a not particularly revealing graphical representation this state might look something like this:

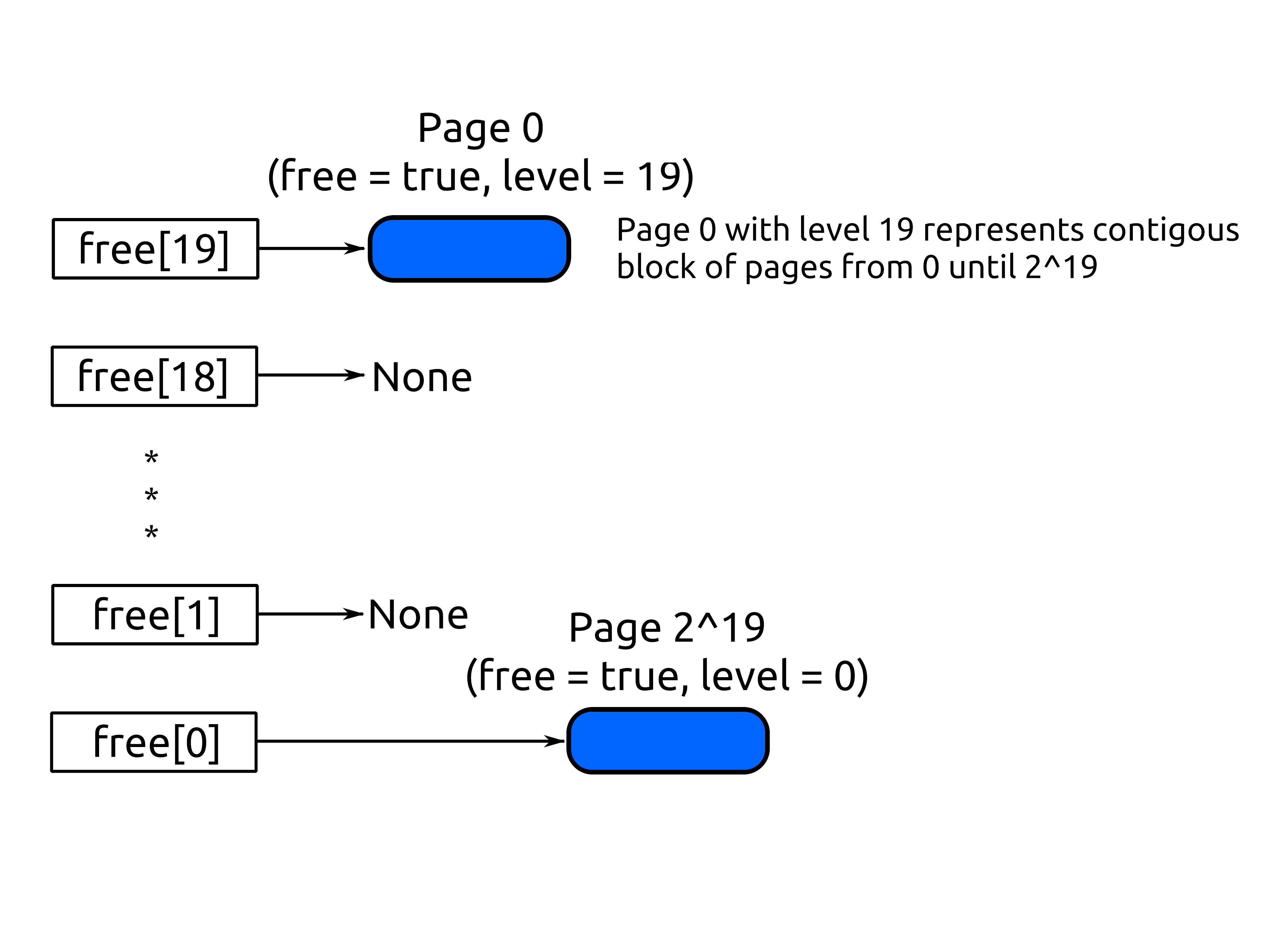
Now, what if add one more page to the system, so that we have \(2^{19} + 1\) pages of memory in total and all of them are free?

In this case, and you can check it for yourself, this additional page will not have buddies at any level - it will be a loner page. That means that it cannot be combined with any other page and as a result can only be a part of a block of level 0 (block that consists of just that one page).

So the state with this additional page will be almost the same as the state we looked at before. However in addition to the free[19] begin not empty, free[0] also will not be empty. free[0] will contain just one element containing that one additional page. The Page structure for that page will be marked as free and will have the level set to 0.

Adding this one page will change our graphical representation to this:

Now, when we have some intuition about how the sate of the algorithm is tracked let’s get to the allocation itself. The allocation will proceed in two stages:

1. finding a large enough free block;
2. splitting the block in smaller blocks.

Finding a large enough free block

Let’s assume that we want to allocate \(2^x\) pages (we call allocate_pages(x)), where \(x\) is anywhere between 0 and 19. We first have to take a look at the free[x] list and check if it’s empty or not. If the list is not empty, then it means that we have a free block of size exactly \(2^x\). In this case we can just remove the element from the list, mark it as busy and return to the caller the index of the first page in that block.

However, it might happen that the free[x] is empty. In this case we assume that we don’t have a free block of size exactly \(2^x\) available. We might have bigger blocks available though. So we should check other free lists starting from \(x + 1\) until we find a non empty list (if there is one of course).

If all the lists are empty, we conclude that there is no large enough free block to satisfy our request.

NOTE: We might in fact have a large enough contigous free block to satisfy the request. Consider the case when we have only pages 1 and 2 free and we want to allocate block of level 1. Since pages 1 and 2 are neighbours we do have a large enough contigous memory block, however pages 1 and 2 are not buddies according to our definition, so they will not be combined to a larger block by the algorithm.

If we did manage to find a non empty list, then we can just pop any element from that list. The block however might be too big for the request. So to avoid wasting memory we can split the block in two buddies and return one back to the Buddy System. We can repeat this process until we endup with a block of the appropriate size at our hands.

Let’s take a look:

pub fn allocate_pages(&mut self, order: u64) -> Option<u64> {
    unsafe {
        let order = order as usize;
        for level in order..LEVELS {
            if let Some(page) = self.free[level].pop() {
                let index = self.page_index(page);
                assert_eq!(level, page.level());
                self.split_and_return(page, index, order);
                page.set_busy();
                page.set_level(order as u64);
                return Some(index);
            }
        }
        None
    }
}

NOTE: we have to use unsafe code here because we are performing address arithmetic here which is unsafe in Rust and because List operations are unsafe. However all of those are internal details of implementation and don’t leave the function, so it’s fine to mark the whole function as safe.

The general flow of the function is straighforward - we start at the free list responsible for the order order and work our way upwards, until we run out of free lists or find a free list with elements.

Helper function page_index converts a reference to the Page structure to its index. It can be done using basic pointer arithmetics, since all the Page structures are stored in the same slice and we know where the slice begins.

The split_and_return function is responsible for the second stage of our algorithm. If we found a free block, but it’s too large, split_and_return will repeatedly split the block in two buddies and return the buddies we don’t need back to the Buddy System.

Once we are done, we have to mark the block as busy. We do it by marking the representative of the block as busy and recording the level of the block in the Page structure.

Splitting the block in smaller blocks

Now let’s take a look at how split_and_return function works. You probably can guess that it works in the opposite direction compared to the allocate_pages - it starts from a higher level and then works it way towards lower levels.

As input the split_and_return function gets the representative of the free block we found and its index as well as the target level that the caller requested.

Here is how it goes:

unsafe fn split_and_return(&mut self, page: &Page, index: u64, order: usize) {
    let from = page.level() as usize;
    let to = order;

    for level in (to..from).rev() {
        let buddy = &self.pages[BuddySystem::buddy_index(index, level)];

        buddy.set_level(level as u64);
        buddy.set_free();
        self.free[level].push(buddy);
    }
}

Here BuddySystem::buddy_index is a helper function that calculates a buddy index at a give level using the formula we saw above.

So again, the function is not really tricky. It’s given a large block. It splits it in two smaller buddies. One of the buddies go back to the appropriate free list, and the function keep working with the other one. The function keep spliting blocks until it ends up with a block of required size.

For the buddies that the function returns back to the Buddy System it’s important to not just mark them as free, but also set the right level there. It is important for the correct freeing logic, which I’ll cover later, but it’s also important for the implementation of the split_and_return function presented here.

The function depends on page.level() returning the correct value. split_and_return uses page.level() to figure out the level it started from.

And that’s it - it’s the complete allocation implementation. That’s not terribly a lot of code.

You can easily see that the number of operations grows with the size of the free array inside the BuddySystem structure. That’s a serious improvment over the algorithm detailed in the previous post where the free list can be arbitrary long.

We achived this improvement by segregating one large free list into a few smaller free list by the powers of two. You can actually take the same idea of segregating a free list and combine it with the algorithm described in the previous post and don’t bother with all the buddy stuff.

That being said, the implementation is likely to be quite a bit more complicatedthan what you have here with the Buddy System.

Freeing pages

To free pages we need to do the opposite operation. For the block we want to free we need to check if the buddy of the block is also free. If the buddy is free, then we can combine them in a bigger block and repeat the operation.

There are a few caveats that you should keep in mind here. First of all, we need to be careful how we check that the buddy is free. Secondly, we need to keep in mind that some blocks may not even have a buddy at all, as we saw in the example above when we had an odd number of pages.

Let’s start with the second caveat. How can we check that the buddy at a certain level even exists? It’s actually quite easy, all we need to do is to find the index of the hypothetical buddy. If this index points to a page that actually exists, then you have your buddy, otherwise you don’t.

As for the checking if the buddy is free, you obviously have to check if the buddy page is marked as free. However it’s not enough. The caveat comes from the fact that a page might be free, but have a wrong level.

Let’s take a look at an example to demonstrate this case. We will look at four pages: 0, 1, 2, 3. Pages 0 and 1 are level 0 buddies, pages 2 and 3 are level 0 buddies, pages 0 and 2 are level 1 buddies - all of that following the buddy definition above.

Now let’s say that page 0 is free, but page 1 is not, like on this picture:

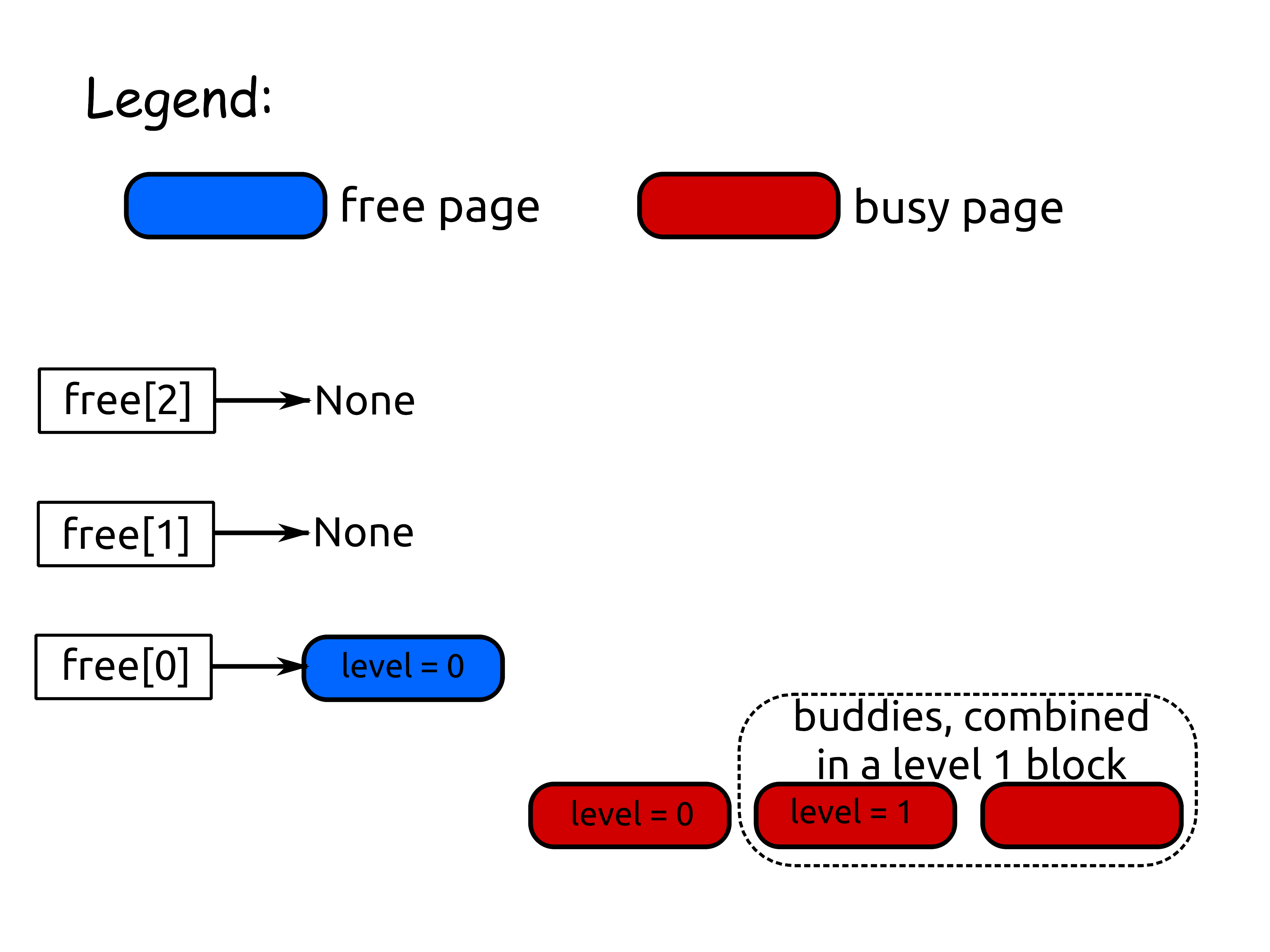
With this state in mind, imagine that we want to free a block of order 1 that starts from page 2 (so block that contains pages 2 and 3). We check the buddy of page 2 at the level 1 and the buddy index is 0, so we have to look at page 0. And surprise! Page 0 is actually free!

However, because page 1 is not free, the block of order 1 starting at the page 0 as a whole is not free. So we cannot combine two blocks of order 1 in one block of order 2.

After freeing operation completes correctly the sate we should have should look like this:

See how pages 3 and 4 ended up in the free list at the level 1 and the page 0 stayed in the list at the level 0. The only way those can be combined is if we free the page 1, that is not free at the moment.

So to avoid this problem in this situation we have to check both the free bit and the level of the page. In the example above, page 0 is free, but its level is 0 and not 1 as we need.

The rest is purely technical stuff:

use core::cmp;

pub fn free_pages(&mut self, index: u64) {
    let mut index = index;
    let mut level = self.pages[index].level() as usize;

    unsafe {
        while level < LEVELS - 1 {
            let buddy = BuddySystem::buddy_index(index, level);

            if buddy >= self.pages.len() {
                break;
            }

            let page = &self.pages[buddy];
            if !page.is_free() { break; }
            if page.level() as usize != level { break; }

            self.free[level].remove(page);
            // representative of the block is always the first page in that
            // block, so we need to pick the smallest index from two buddies
            index = cmp::min(index, buddy);
            level += 1;
        }

        let page = &self.pages[index];
        page.set_free();
        page.set_level(level as u64);
        self.free[level].push(page);
    }
}

Again, the whole implementation just fits in a few lines of code. And again it’s not hard to see that each iteration of the loop takes constant time and the number of iterations is bounded by the number of elements in the free array.

This time we could not say that it’s a win of the approach described in the previous post since there freeing memory was a constant time operation. That being said, given that the size of free array is very much bounded, we are not far behind.

Instead of conclusion

The implementation I presented in this post is slightly different from the implementation you’ll find in the repository. That being said you should still be able to recognize the overall algorithm.

The reason why the implementation in the repository is different is because it enforces an additional alignment restriction: when you allocate \(2^x\) pages it makes sure that the result is aligned on the \(2^x\) boundary as well. Due to the way BuddySystem works, this alignment property comes almost for free with only a slight modification of the implementation.

As I mentioned before, Buddy System is quite practical algorithm, in the sense that it’s in fact used quite a lot. For example, it’s used in the Linux Kernel for memory pages allocation and it served as a building block of generic memory allocator known as jemalloc.

Buddy System also serves as a simple enough introduction into the idea of segregated free lists. This is an important approach for modern efficient memory allocators. For example. another popular generic memory allocator tcmalloc doesn’t use the Buddy System approach for splitting and coalescing memory blocks, but does heavily employ segregated free lists.

So all-in-all, it’s quite useful algorithm to understand.