Dynamic Memory Allocation Part3

I didn’t post for quite some time. In the previous post I covered buddy allocator. Buddy allocator, while begin a an actually practical algorithm, has it’s limitations.

One obvious limitation is that it allocates memory in multiples of the basic block size. Moreover the multiplier has to be a power of 2. That will lead to some memory wasted if you want to allocate a memory chunk that is not a power of 2 multiple of the basic block size.

Another caveat is the data that we need to maintain for bookkeeping. In the specifc implementation I showed I pre-allocated a page structure for each basic block. This page structure is a bit above 16 bytes in size and the smaller the base block is the more such structures we need. Which increases the overhead of the buddy allocator if we want to allocate small chunks of memory.

So here I’m going to cover another approach to memory allocation that is more efficient when working with smaller object sizes.

I take no creadit for the algorithm itself. This post covers a very simplified version of an algorithm proposed by Jeff Bonwick and described in the The SLAB Allocator paper.

As always the code is available on GitHub.

Introduction

First of all, we will start from simplifing the problem. The most generic interface a memory allocator can have may contain just a couple of methods:

void* allocate(size_t size);
void free(void* ptr);

Basically we tell allocator the amount of memory we need and it gives us a ppointer to a large enough memory chunk. We are going to abandon this idea that we need to be able to allocate memory chunks of different size.

Instead we will create an allocator that is only capable of allocating of memory chunks of single fixed size. So when we will create an allocator we will instruct it what size it will support and that size will stay the same throughout the lifetime of the allocator.

I will go even further and simplify our task even more and assume that we already have an allocator that we can use to allocate large chunks of memory. For example, we could use a Buddy allocator or any other similar algorithm.

With such a simplified problem statement, all we really need is to allocate memory for a large array of objects of the same size and keep track which one have been allocated already and which are still free.

SLAB

I think you got the general idea of what we are going to do, let’s flash out some details of how exactly are we going to do that. First, we will organize our memory in a set of SLABs.

Each SLAB will contain the array of objects of a fixed size plus some bookkeeping structures to keep track of what of the objects are free and what are busy.

Connecting it back to the general idea covered above, SLAB will be our array of objects. Once one SLAB gets full, we can allocate a new SLAB. If we freed all of the objects in the SLAB we can free the whole SLAB back.

There are multiple different layouts that a SLAB can use, here is the high level idea of the layout I use in my simplified example:

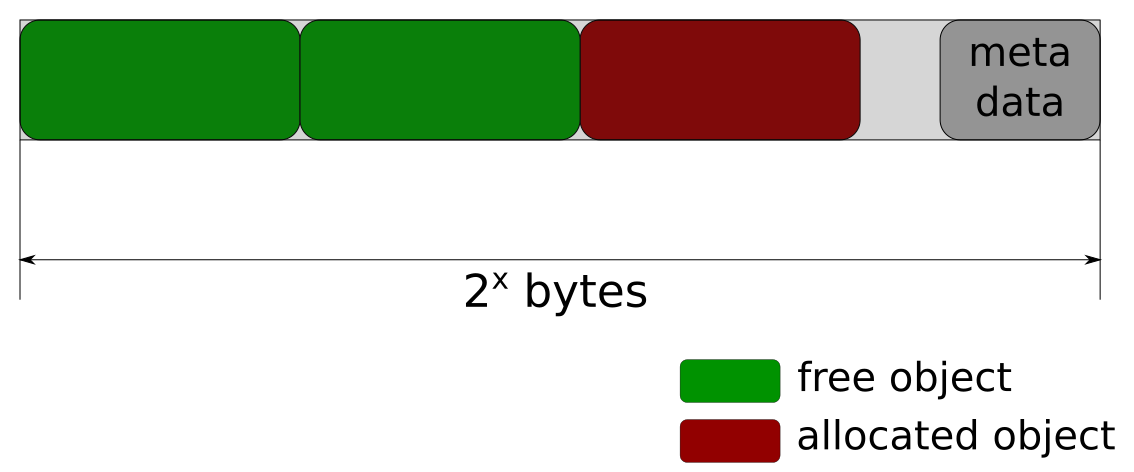
NOTE: I decided that a SLAB size has to be a power of 2 and has to be aligned on the power of 2 boundary. It works nicely with the Buddy allocator I described in [the previous post], but that’s not the reason why it was decided this way. I will cover the purpose of that later in the post.

On the picture you can see that I have an array of fixed size memory chunks in the SLAB. Some of them are free and some of them are occupied.

Initially, when we create a new SLAB, all of those objects will be free and as we allocate and free objects from the SLAB we can get various combinations of free and busy objects.

Naturally, we need to keep track what objects are free and what objects are busy. In order to do that I will organize all the free objects in the SLAB into a linked list.

When an object is free, all the memory is available for us to use. So I keep all the pointers required to organize objects in a list right in that very memory that the object occupies. So each object should be large enough to store a pointer, so that we can organize objects in a list.

So here is what I used in my code:

struct Storage : public common::ListNode<Storage> {
    void* pointer;

    Storage(void* ptr) : pointer(ptr) {}
};

NOTE: common::ListNode is a C++ template representing a node of an intrusive linked list, so I can derrive from it and then organize objects in a linked list - I’m not going to cover it in more details, but you’ll see in code examples how the list is used.

NOTE: pointer is just a pointer to the beginning of the object in the free list. Strictly speaking we don’t really need it, because we can just type cast pointer to the Storage object directly to void*. It’s more of my personal taste to avoid type casts if possible.

So for free objects in the SLAB we have something like this in memory:

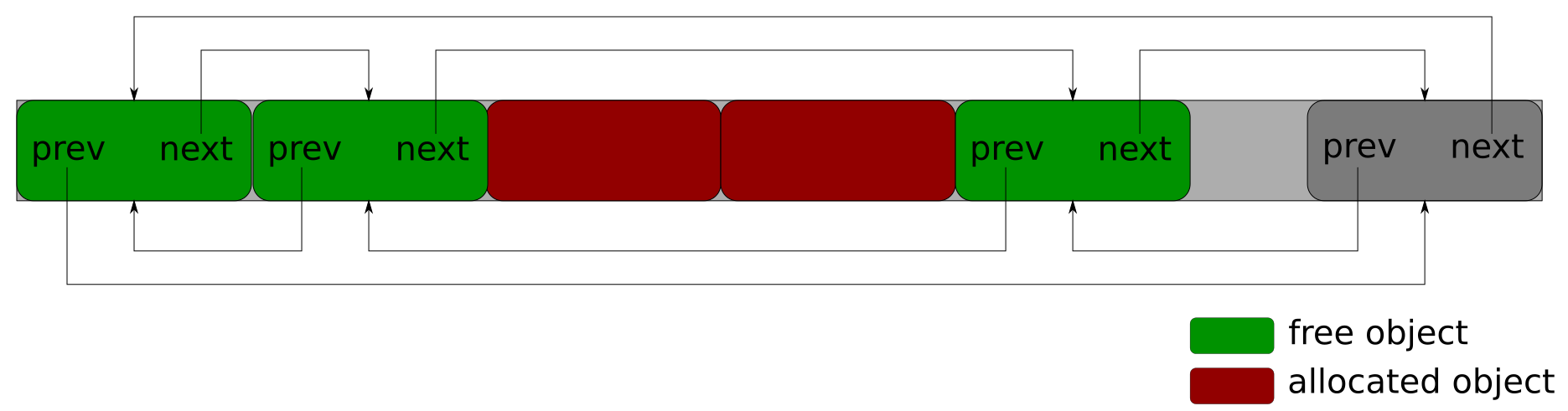
NOTE: My layout is actually quite different from what Bonwick proposed. My layout is simpler and because of that does not allow for some performance optimizations that Bonwick covered in the orignal paper.

NOTE: Doubly linked list is not actually needed here, a singly linked list is just enough to link the free objects in the list.

When we allocate we take an object from the list, when we free we return an object back to the list - that’s it.

Besides the array of objects, each SLAB will have some metadata. Obviously we need to store the head of the free objects list somewhere, so we will store it in our metadata. This free list is the only thing we need to allocate/free objects from/back to the SLAB.

There are a few things that I will add on top of that to our metadata:

• counter of the number of allocated objects;
• range of memory addresses that the SLAB occupies;
• pointer back to the allocator that the SLAB belongs to.

None of that is strictly needed for the allocator itself, but I think they might be useful for various internal integrity checks, statistics and so on.

In the end the SLAB metadata looks like this:

class Slab : public common::ListNode<Slab> {
public:

    void* Allocate();
    bool Free(void* ptr);

    /* Some other methods here */

private:
    /* The actual data */
    common::IntrusiveList<Storage> freelist_;
    size_t allocated_ = 0;
    /*
     * Cache is the name of the allocator class in my code.
     * For now the details of the Cache class do not matter.
     */
    const Cache* cache_ = nullptr;
    /*
     * Contigous is a structure that describes a contigous chunk of memory.
     * In this case memory_ describes the memory that this very SLAB occupies
     * (inlcuding the array of objects, metadata, all of it).
     */
    Contigous memory_;
};

NOTE: As you can figure out from the fact that Slab inherits common::ListNode<Slab>, we want to organize SLABs in a linked list, you will see later why it’s the case.

Working with SLABs

Now let’s take a look at how we can allocate some memory from a SLAB. Well, it’s quite trivial - we have a list of free object, let’s just take the first object from the list and return it.

void* Slab::Allocate() {
    Storage* storage = freelist_.PopFront();
    if (storage == nullptr) {
        return nullptr;
    }

    void* ptr = storage->pointer;
    storage->~Storage();
    ++allocated_;
    return ptr;
}

I stress here again that, in contrast to other allocation algorithms that I covered, we do not specify the amount of memory we want to allocate.

Each SLAB can only allocate objects of a fixed size. The size of the objects it can allocate is fixed at the time of allocator creation and cannot change after that. Exactly because of that limitation we can have such a simple allocation routine.

Now, let’s take a look at how to free an object back to the SLAB. It’s not much more complicated than the Allocate function above:

bool Slab::Free(void* ptr) {
    const uintptr_t addr = reinterpret_cast<uintptr_t>(ptr);
    if (addr < memory_.FromAddress() || addr >= memory_.ToAddress()) {
        return false;
    }

    Storage* storage = reinterpret_cast<Storage*>(ptr);
    ::new (storage) Storage(ptr);
    freelist_.PushFront(storage);
    --allocated_;
    return true;
}

NOTE: checking whether address belongs to the memory range is not really required by the algorithm itself, it’s just an internal integrity check to try to catch incorrect use of the algorithm and the bugs in the implementation. Similar story with returning bool from the function.

SLAB management

Working with the SLABs is easy once you have them, but how do we create and destroy SLABs? I will start with the following helper class that will be responsible for allocating, finding and freeing SLABs.

struct Layout {
    size_t object_size;
    size_t object_offset;
    size_t objects;
    size_t control_offset;
    size_t slab_size;
};

class Allocator {
public:
    Allocator(Layout layout);

    ...

    Slab* Allocate(const Cache* cache);
    void Free(Slab* slab);
    Slab* Find(void* ptr);

private:
    /* some bookkeeping information */
};

Let’s first explain what Layout struct is for. It’s a structure that describes the layout of the SLAB:

• the size of the SLAB
• the size and the number of objects we can allocate from the SLAB
• where the allocated objects are located inside the SLAB
• where the metadata located inside the SLAB
• etc.

When we create a SLAB we use this information to initialize the SLAB, let’s take a look at the SLAB constructor to see how it looks:

Slab::Slab(const Cache* cache, Contigous mem, Layout layout)
        : cache_(cache), memory_(mem) {
    const uintptr_t from = memory_.FromAddress() + layout.object_offset;
    const uintptr_t to = from _ layout.object_size * layout.objects;

    for (uintptr_t addr = from; addr < to; addr += layout.object_size) {
        void* ptr = reinterpret_cast<void*>(addr);
        Storage* storage = reinterpret_cast<Storage*>(ptr);
        ::new (storage) Storage(ptr);
        freelist_.PushBack(storage);
    }
}

So all-in-all, SLAB initialization boils down to a bunch of memory pointer casts to create the list of free object that we use for allocating from the SLAB as was shown above.

Now we know how to initialize a new SLAB, let’s now take a look at the Allocator:

Allocator::Allocator(Layout layout) : layout_(layout) {}

Slab* Allocator::Allocate(const Cache* cache) {
    Contigous memory = AllocatePhysical(layout_.slab_size).release();
    if (!memory.Size()) {
        return nullptr;
    }

    Slab* slab = reinterpret_cast<Slab*>(
            memory.FromAddress() + layout_.control_offset);
    ::new (slab) Slab(cache, memory, layout_);
    return slab;
}

This snippet is a bit complicated, because I skipped through a few background details. Let’s try to explain them now. AllocatePhysical is C++ implementation of Buddy allocator that I use and it returns a structure called Contigous that describes a contigous range of memory allocated by the allocator.

The rest should be more or less understandable. Once we allocated a contigous memory chunk for the SLAB, we find the offset of metadata inside it (based on the Layout structure) and initialize Slab object there. SLAB constructor does most of the work and you saw it above already.

Freeing a SLAB is also rather straightforward:

void Allocator::Free(Slab* slab) {
    Contigous memory = slab->Memory();
    slab->~Slab();
    FreePhysical(memory);
}

NOTE: we get a copy of Contigous structure from the SLAB before calling a destructor, since we should not access any members of the object after it was destroyed.

As you probably guessed, FreePhysical is the function that returns memory back to the Buddy allocator.

Finally, we need the Find function. The purpose of this function is to find a SLAB that contains a certain pointer. Why do we need it? You will see the details later, but in short we could have multiple SLABs at the same time. When we want to free some memory that was allocated from a SLAB we need to find the SLAB from which we allocated that memory. That’s why we need the Find function.

How can we implement Find function? The origianl SLAB allocator paper suggested to maintain a hash map. Using a hash map would work, but somewhat complicated, so I went for a bit simpler and significantly hackier option instead.

Remember that we use Buddy allocator to allocate SLABs. Buddy allocator allocates objects of size that is a power of 2. Additionally, it’s possible to implement Buddy allocator in such a way, that it will allocate objects of size $2^x$ aligned on the boundary of $2^x$. That alignment propery allows us to use a nifty trick:

Slab* Allocator::Find(void* ptr) {
    const uintptr_t addr = reinterpret_cast<uintptr_t>(ptr);
    const uintptr_t head = common::AlignDown(
        addr, static_cast<uintptr_t>(layout_.slab_size));
    Slab* slab = reinterpret_cast<Slab*>(head + layout_.control_offset);
    Contigous memory = slab->Memory();
    if (addr < memory.FromAddress() || addr >= memory.ToAddress()) {
        return nullptr;
    }
    return slab;
}

Let’s quickly look at the implementation of the AlignDown function:

template <typename T>
T AlignDown(T x, T alignment) {
    return x & ~(alignment - 1);
}

So essentially, what the Find function does it just finds the closest address that is:

1. less then or equal to the value of ptr
2. is aligned on the SLAB size boundary.

We add a quick check on top of it to make sure that we are not looking at some random memory that never contained SLAB in the first place and that’s it.

Does it look shady? Well, it’s because it is absolutely shady.

Layout

Before we jump to the final part, let’s take a look at the Layout structure. So far we just assumed that it exists and it’s populated with values that make sense. Now we will look at how can we initialize the Layout structure.

We have 2 input parameters that control the layout of our SLABs:

1. the size of the object we want to allocate from the SLAB (remember that we allocate objects of a fixed size)
2. the alignment of the object we want to allocate.

The alignment argument is a bit of a technical detail, but some hardware architectures may require memory to be aligned on a certain boundary.

For example, if your code tries to load 4 bytes long piece of data from memory to a register, CPU may require that that those 4 bytes of data are located in memory starting at the address divisble by 4. For the algorithm it does not really matter why such restrictions may exist - we just have to support them, because otherwise the memory we return from the allocator may not be usable.

How can we account for the alignment constraints? Well, obviously we need to put our objects in the SLAB starting from the address aligned on the right boundary. However that’s not enough.

Consider a situation when you need to allocate objects that are 16 bytes long, but for whatever reason they have to be aligned on the 32 bytes boundary. Even if you put the first object on the 16 bytes boundary, the next object that is located right after the first one will not be aligned to a 16 bytes boundary.

So to account for that, we need to keep some gap between the objects to make sure that all of them are aligned on the right boundary. In other words, we need to artificially increase the size of the object.

Additionally on top of that, all our objects have to be at least large enough to contain Storage structure, so that we could link them into a list. Putting everything together gives us something like this:

size_t ObjectSize(size_t size, size_t alignment) {
    return common::AlignUp(std::max(size, sizeof(Storage)), alignment);
}

The second thing we need to figure out is how big each SLAB should be. There is quite a bit of flexibility there. One thing that I considered is how much memory will be wasted depending on the size of the SLAB.

Imagine we allocate a SLAB that is just 4096 bytes large. It needs to contain the SLAB metadata and all the objects within 4096 bytes chunk of memory. Let’s also assume that the size of the SLAB metadata is 64 bytes and the size of the object is 2048 bytes. With this parameters we will be able to allocate only a single object per SLAB, which is already not great, but on top of that 1984 bytes will not store anything and will be basically wasted. That’s almost 50% of the total memory we allocate for the SLAB.

On the other hand, if the SLAB was 32768 bytes long. We would be able to fit there SLAB metadata and 15 objects of size 2048. In this case we again will waste 1984 bytes, but comparing it to the size of the SLAB it’s just about 6% of the total memory we allocate for the SLAB, which is much better.

So the bigger SLAB we allocate the less memory we waste. On the other hand if we allocate a SLAB that it’s too large and don’t use all the objects there we would also be wasting memory.

With that background out of the way, here is the heuristic I came up with:

size_t SlabSize(size_t size, size_t control) {
    constexpr size_t kMinObjects = 8;
    constexpr size_t kMinSize = 4096;

    const size_t min_bytes = size * kMinObjects + control;

    if (kMinSize >= min_bytes) {
        return kMinSize;
    }

    const size_t order = common::MostSignificantBit(min_bytes - 1) + 1;
    return static_cast<size_t>(1) << order;
}

And the final code that will define the layout of a SLAB looks like this:

Layout MakeLayout(size_t size, size_t alignment) {
    const size_t control_size = sizeof(Slab);
    const size_t object_size = ObjectSize(size, alignment);
    const size_t slab_size = SlabSize(object_size, control_size);

    Layout layout;
    layout.object_size = object_size;
    layout.object_offset = 0;
    layout.objects = (slab_size - control_size) / object_size;
    layout.control_offset = slab_size - control_size;
    layout.slab_size = slab_size;
    return layout;
}

Aside from the topics we covered above, two things that are relevant here. Given that we use Buddy allocator to allocate a SLAB, the SLAB size have to be a power of 2 and will be aligned in memory on the power of 2 boundary. That means that if we put our objects at the beginning of the SLAB, the first of the objects will be aligned on the power of 2 boundary. Similarly, if we put something at the end of the SLAB, it will be aligned well.

In this case I put objects at the beginning of the SLAB memory range and put the SLAB metadata at the end of the SLAB memory range, thus everything should be well aligned inside the SLAB.

Cache

We have most of our building blocks ready to create the final allocator. Let’s see how the interface of our allocator will look like:

class Cache {
public:
    Cache(size_t size, size_t alignment);

    void* Allocate();
    bool Free(void* ptr);
    bool Reclaim();

private:
    /* some fields that will be covered later */
};

Allocate and Free are self explanatory, Reclaim requires a bit of a clarification. As you may have noticed, SLAB is more of a memory cache rather than a true memory allocator (thus the name of the class). It would be useful to have an option to tell to the cache to release the memory it doesn’t need now back to the system. That’s exactly what the Reclaim function is for.

Inside our Cache we are going to maintain 3 lists of SLABs:

• SLABs that are full - we cannot allocate anything from those anymore
• SLABs that are empty - we can return those back to the system if needed
• SLABs that are not full and not empty (partial) - we cannot return those back to the system and we can allocate some objects from them.

class Cache {
public:
    Cache(size_t size, size_t alignment);

    void* Allocate();
    bool Free(void* ptr);
    bool Reclaim();

private:
    Layout layout_;
    Allocator allocator_;
    common::IntrusiveList<Slab> free_;
    common::IntrusiveList<Slab> partial_;
    common::IntrusiveList<Slab> full_;
};

When we need to allocate a new object, we will first check the partially used SLABs. If there are none, we will check the empty SLABs. If there are none we will create a new SLAB.

When we free an object we will always have to free it to the same SLAB from which we allocated it in the first place. However, freeing an object may turn SLAB from full to partially used or from partially used to empty. So we will have to move the SLABs between the list accordingly.

Fortunately, we maintain SLABs in linked lists, so it’s not that hard to do. Let’s take a look:

void* Cache::Allocate() {
    if (!partial_.Empty()) {
        Slab* slab = partial_.Front();
        if (slab->Allocated() + 1 == layout_.objects) {
            partial_.Unlink(slab);
            full_.PushFront(slab);
        }
        return slab->Allocate();
    }

    if (!free_.Empty()) {
        Slab* slab = free_.PopFront();
        partial_.PushFront(slab);
        return slab->Allocate();
    }

    Slab* slab = allocator_.Allocate(this);
    if (slab == nullptr) {
        return nullptr;
    }

    partial_.PushFront(slab);
    return slab->Allocate();
}

bool Cache::Free(void* ptr) {
    if (ptr == nullptr) {
        return false;
    }

    Slab* slab = allocator_.Find(ptr);
    if (slab == nullptr) {
        return false;
    }

    if (slab->Owner() != this) {
        Panic();
    }

    if (slab->Allocated() == 0) {
        return false;
    }

    if (!slab->Free(ptr)) {
        return false;
    }

    if (slab->Allocated() == 0) {
        partial_.Unlink(slab);
        free_.PushFront(slab);
    }

    if (slab->Allocated() + 1 == layout_.objects) {
        full_.Unlink(slab);
        partial_.PushFront(slab);
    }

    return true;
}

NOTE: I brushed over the details of how we check if the SLAB is full or empty, but hopefully it will not be too much trouble to figure out how to implement the Allocated function for the SLAB by just maintaing a counter of the objects that were allocated from the SLAB.

NOTE: Half of the Free function are various internal integrity checks that have little to do with the algorithm itself, that’s why it looks more complicated than it actually is.

Where to go from here

This is the most basic skeleton of a SLAB-like memory allocator. Most of the functions of the SLAB allocator only require a constant amount of time to finish until we need to allocate or free a SLAB. By allocating large enough SLABs we can amortize the cost of allocating and freeing SLABs and bring the amortized cost of allocation and deallocation to constant time with SLABs. So that is pretty nice in its own right, compared to the naive memory allocators that I covered before.

However SLAB can offer much more than that. If you refer to the orignal paper you will find a few interesting optimizations that could be applied to the SLAB allocator and some idea of the impact that those optimizations provide. I’m not going to cover those here because my implementation was simplified to such an extend that it cannot support some of those anymore.

However, I think it might be useful to give you an idea how to build a generic memory allocator, an allocator that can allocate objects of different sizes, using SLAB allocator.

Essentially you can pre-create SLAB allocators for object of different sizes in advance. When we need to allocate memory we first find the smallest SLAB allocator that fits and allocate the object from that SLAB allocator. That’s quite easy.

When we free memory back we need to find the SLAB allocator we allocated it from. This might be a bit complicated, but not impossible to figure out. One simple idea that we could use here is to do some bookkeeping during allocation. For example, we can allocate a bit more memory then requested. In the additional memory we can save the Cache pointer for later. A hash table will work fine as well.

So using a SLAB allocator we can create a generic memory allocator that takes an amortized constant time to allocate and free memory of any size, which is quite neat.

Instead of conclusion

The original SLAB allocator is quite complicated, powerful and efficient algorithm. However, the fundamental ideas behind the algorithm are quite easy to understand and use.

Variations of top of SLAB algorithm are used in all kinds of systems and generic memory allocators, so it’s quite a useful algorithm to understand.

Naturally, this post just scratches over the surface, but hopefully it will be enough to get you started to explore the details on your own.

I’m probably not going to cover anything else related to memory allocation and instead will switch to ARM specific topics like how virtual memory works in ARM in the future posts.